Сейнов С.В., д.т.н., проф., чл.-корр. РАПК, Пензенский государственный университет, президент-научный руководитель НПО «ГАКС-АРМСЕРВИС»,
Сейнов Ю.С., вице-президент НПО «ГАКС-АРМСЕРВИС»
С целью оптимизации выбора трубопроводной арматуры для различных производственных объектов в России, как и, за рубежом используются нормативные документы. Они регламентируют герметичность затвора по десяти классам в зависимости от величины утечки транспортируемой или пробной среды. Не вдаваясь в физическую сущность установленных ограничений по утечке, производитель должен решить проблему управления процессом герметизации применительно к каждому классу. В настоящее время арматуростроители используют три основных метода обеспечения герметичности затвора. Первый – силовой, основанный на контактном давлении герметизации в уплотнении затвора, которое зависит от геометрической формы его элементов. Второй – размерно-геометрический, опирающийся на оптимизацию выбора исходных значений метрических параметров уплотнений, учитывающий закономерности формирования межуплотнительного пространства, позволяющих обеспечивать необходимые его размеры, гарантирующие величины утечек, предписанные каждому классу герметичности. Третий метод – конструктивный, базирующийся на разработке новых конструкций, создающих, по мнению разработчиков, некие благоприятные условия функционирования затвора и являющихся, чаще всего, частным решением задачи.
Исполнение заданных ограничений по классам герметичности может быть реализовано, по нашему мнению, только на основе второго метода, который позволяет обеспечить эти нормативы и управлять процессом технологическими методами. Это подтверждено многочисленными исследованиями [1, 2], теоретическая часть которых представлена в виде серий графических моделей затвора, системой математических моделей, характеризующих динамику формирования межуплотнительного пространства в затворе и системы математических моделей, позволяющих определить расходные характеристики уплотнения затвора при решении задач материально-энергетического баланса. В основе установления материально-энергетического баланса затвора лежат классические уравнения гидродинамики, преобразованные для решения конкретных задач и выраженные как законы Пуазейля, Дарси, Новье-Стокса, Кнудсона для вязкостного, промежуточного и молекулярного течений.
В качестве исходного принято «квазиточное» соединение элементов уплотнения в затвор различной формы контактного взаимодействия. В нем отсутствуют все погрешности уплотнений в виде шероховатости, волнистости, отклонений формы и взаимного положения, погрешностей линейных и угловых размеров, которые могут появляться в результате формообразования поверхностей и их сборки. Это состояние затвора характеризуется следующими моделями.
Графическая модель затвора
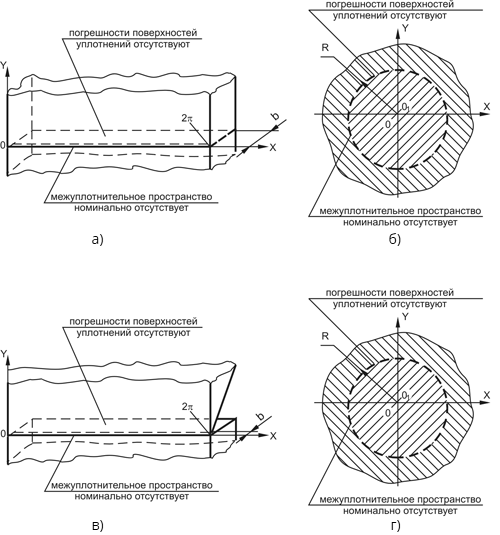
Рис. 1. Квазиточное соединение элементов уплотнения в затвор
а) поверхностное номинальное перекрытие по плоскости (развертка кольца);
б) поверхностное номинальное перекрытие по конусу (сечение, перпендикулярное оси конуса);
в) линейное номинальное перекрытие (ножевой контакт по плоскости);
г) линейное номинальное перекрытие (ножевой контакт на конусе в сечении по линии номинального контакта).
Модель формирования межуплотнительного пространства
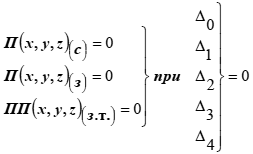
Здесь, П(x, y, z)(c) - функция уплотнительного пространства седла; П(x, y, z)(з) - функция уплотнительного пространства золотника.
ПП(x, y, z)з.т.= ƒ(∆0,1(z)) – функция межуплотнительного пространства от погрешности взаимного положения.
Материально энергетический баланс
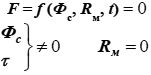
Здесь F – пропускная способность затвора; Фс – комплекс физических составляющих, характеризующих агрегатное состояние транспортируемой среды; t – время, в течение которого оценивается величина утечки, Rм – размерно-геометрические параметры межуплотнительного пространства.
Развитие этой системы моделей было проведено в результате последовательного введения в функции уплотнительного пространства элементов уплотнения и в функции межуплотнительного пространства соединения (затвора) всей совокупности метрических параметров, всегда имеющей место после формообразования и сборки затвора любого конструктивного исполнения.
По результатам экспериментальных исследований взаимосвязи метрических параметров и утечек, установлено следующее.
1. Каждый метрический параметр, входящий в общую совокупность и характеризующий состояние поверхности и их пространственное расположение, оказывают влияние на величину утечки.
2. В определенном диапазоне значений, каждый из метрических параметров имеет «зону нечувствительности» когда этот параметр не оказывает влияния на изменение утечки.
На основе теоретических и экспериментальных исследований была разработана и предложена методология формирования системы допусков для метрических параметров [3], которая позволяет обеспечить соблюдение ограничительных требований по утечкам каждого класса технологическими методами. В основу метода положены:
1. Функциональный принцип формирования системы допусков, когда величина утечки является основополагающим фактором при установлении допуска на управляющий метрический параметр.
2. Принцип однопараметрического управления утечкой для всех классов герметичности, означающей, что управление герметичностью должно осуществляться за счет только одного метрического параметра, относящегося к высокочастотным составляющим спектра неровностей.
3. Принцип постоянства и полноты всей совокупности допусков для всех классов герметичности по не управляющим метрическим параметрам, к которым отнесены низкочастотные составляющие спектра неровности, имеющих «зоны нечувствительности» по их влиянию на утечку.
Методология формирования системы функциональных допусков метрических параметров может быть представлена структурой (рис. 2) и функцией оптимизации.
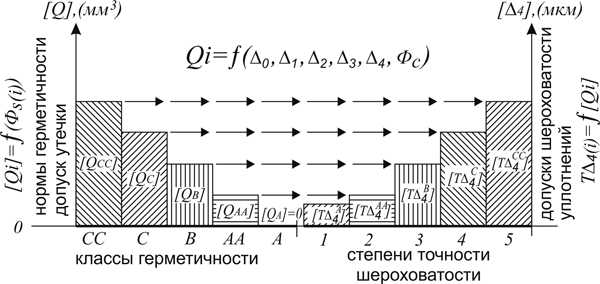
Рис. 2. Структурная схема методологии формирования системы функциональных допусков метрических параметров
На схеме:
ƒ(ФS(i)) - функция, характеризующая утечку, которая оказывает влияние на физический процесс в герметизируемой системе.
T∆4(i) - допуск управляющего параметра – шероховатости уплотнений как функция допуска утечки затвора.
Qi = f(∆0, ∆1, ∆2, ∆3, ∆4, Фс) – базовая зависимость утечки от полной совокупности функциональных метрических параметров уплотнений.
Функция оптимизации имеет вид:
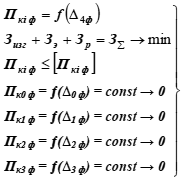
Здесь Пкi ф = ƒ(∆4ф) – управление связи показателя качества (утечки) с управляющим параметром его обеспечения;
Зизг + Зэ + Зр = З∑ → min – функция цели оптимизации;
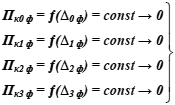 |
- Совокупность оптимизационных ограничений, вытекающих из третьего принципа методологии нормирования.
|
Результатом решения оптимизационной задачи, теоретических и экспериментальных исследований явились нормативы функциональных метрических параметров, широко используемых в практической деятельности НПО «ГАКС-АРМСЕРВИС» и внесены в некоторые отраслевые стандарты.
Выводы
1. Нормирование метрических параметров уплотнений является действенным механизмом технологического управления процессом герметизации затвора только в том случае, если нормированием охвачена вся совокупность этих параметров.
2. Одной из главных проблем широкого промышленного внедрения нормативов на функциональные метрические параметры и технологических процессов их обеспечения является неудовлетворительное оснащение производства средствами измерения вследствие низкой метрологической культуры.
Литература:
1. Сейнов С.В., Калашников В.А., Железнов Б.П. Испытания трубопроводной арматуры. М.: Стандарты, 1989, 162 с.



